Data structures are fundamental concepts in computer science that enable efficient data organization and manipulation. Today, we will delve into one of the most versatile and widely used data structures: The Tree
What is a Tree
A Tree is a hierarchical data structure that consists of nodes connected by edges. The structure starts at the root node and extends into subtrees by child nodes, with no cycles. Each node contains a value and references to its children.
Key Characteristics of Trees
- Root: the top node in a tree
- Node: an element in the tree that contains a value and references to its children.
- Edge: A connection between two nodes.
- Leaf: A node with no children.
- Subtree: A tree formed by a node and its descendants.
- Height: The length of the longest path from the root to a leaf.
- Depth: The length of the path from the root to a node.
Why should use Tree
Some applications require arranging data in a specific order. For example, when we want an alphabetized list of names of employees in order from A to Z, one solution is to use sorting algorithms like Quicksort with a time complexity of O(NLogN) to arrange our data in ascending order. However, if we need to modify data regularly, the time complexity for inserting or removing data from an array is O(N), which can be quite slow for a simple insertion or deletion. Trees can solve both problems by keeping the array sorted and making search, insertion, and deletion operations faster.
Types of Trees
- Binary Tree: Each node has at most two children, referred to as the the left child and the right child.
- Binary Search Tree (BST): A binary tree with the property that the left child is less than the parent node and the right child is greater than the parent node.
- Balanced Tree: A tree where the height of the left and right subtrees of any node differ by no more than one.
- AVL Tree: A self-balancing binary search tree with addition properties that ensure the tree remain balanced.
- B-Tree: A self-balancing tree data structure that maintains sorted data and allows searches sequential access, insertions, and deletion in logarithmic time.
- Heap: A complete binary tree where the value of each node is greater than or equal to (max heap) or less than or equal to (min heap) that values of its children.
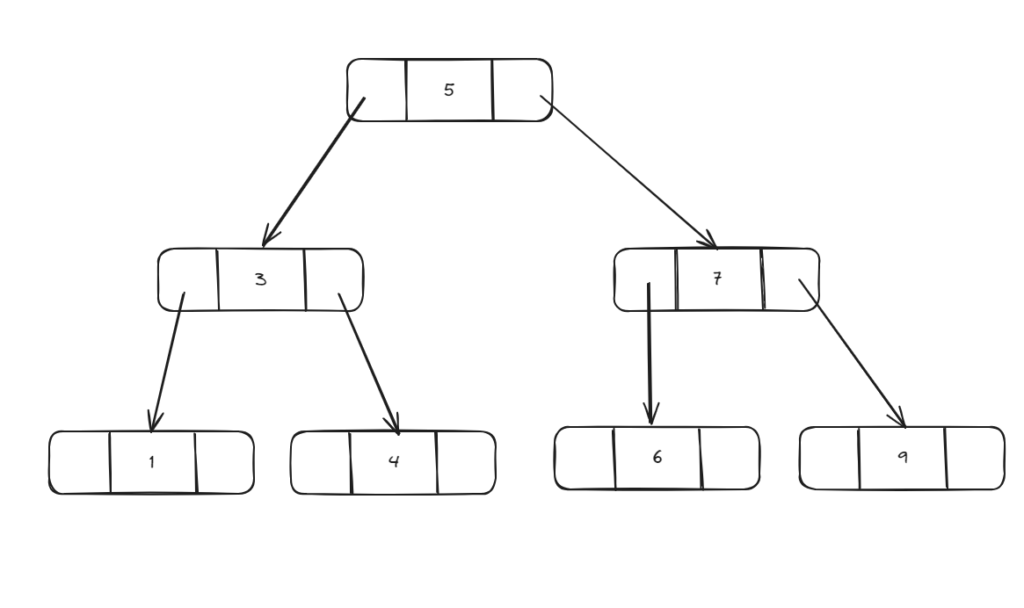
Each node of tree contain :
- Left pointer: point to the next left address of the current node
- Right pointer: point to the next right address of the current node
- Value: Contain value of the current node like number, string, object
Core Operations on Trees
- Insertion: Adding a new node to the tree.
- Deletion: Removing a node from the tree.
- Traversal: visit all the nodes in a specific order.
- In-order Traversal: Left subtree -> Root -> Right subtree
- Pre-order Traversal: Root -> Left subtree -> Right subtree
- Post-order Traversal: Left subtree -> Right subtree -> Root
- Level-order Traversal: Visiting nodes level by level from left to right
Explain why search, insert, delete in BST has time complexity is O(LogN) which is pretty fast
Search element has value 6 in BST like this:

Step 1: Compare 5 < 6 -> go to next right node
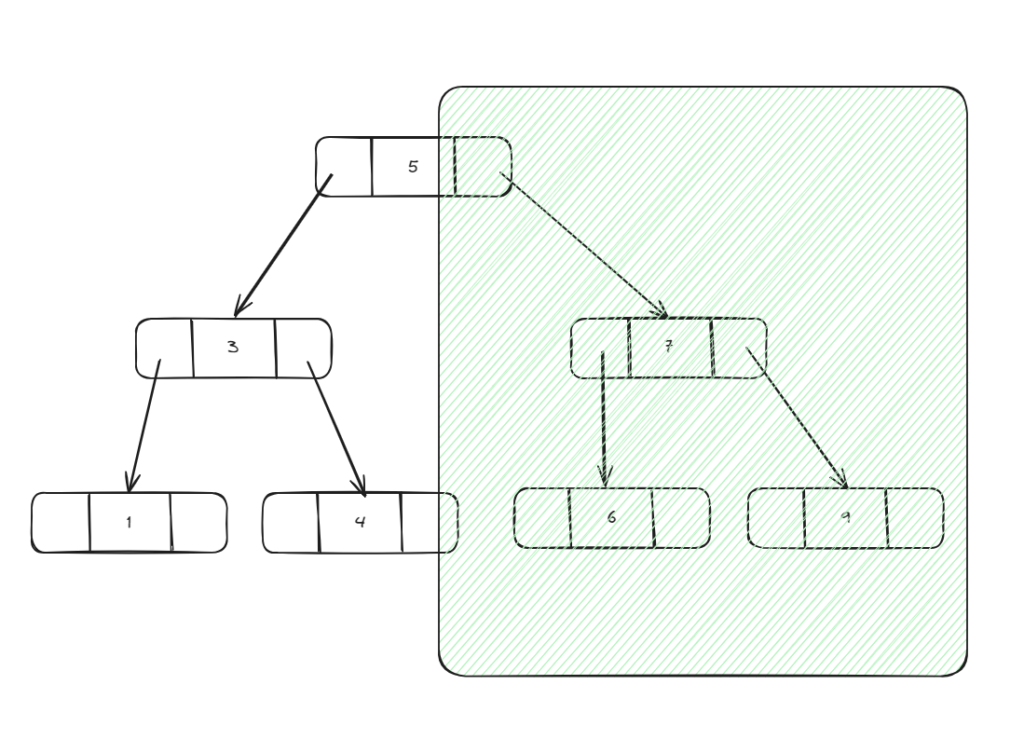
Step 2: compare 7 > 6 -> go to next left node
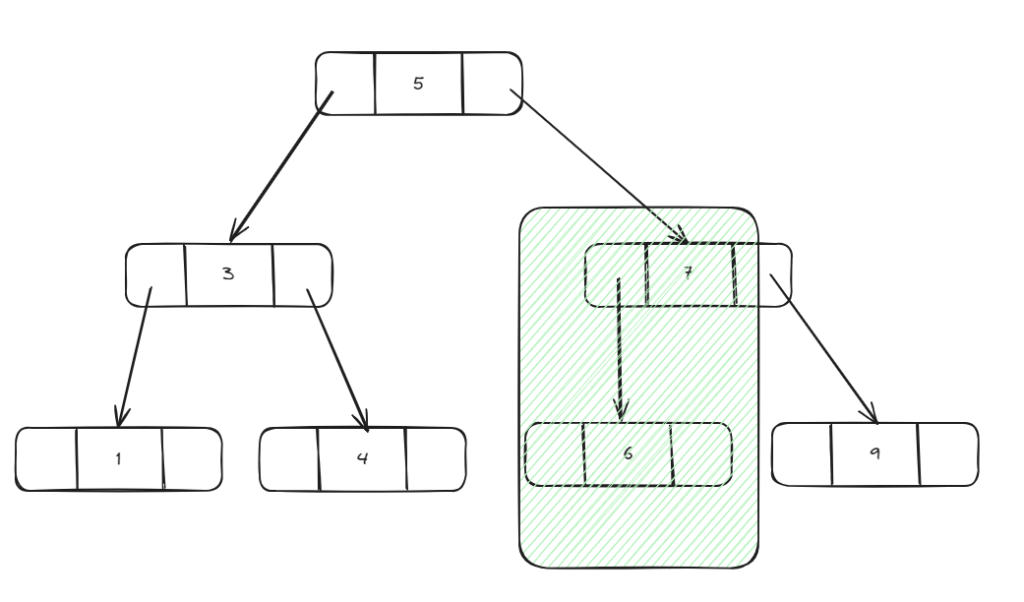
Step 3: We can see 6 = 6 -> found this element
As we can see each step we take we can eliminate half size of left elements we need to search -> O(LogN). The same with insertion and deletion
Use Cases of Trees
Trees are used in various application, such as:
- Hierarchical Data Representation: File systems, organizational structures, and XML/HTML documents.
- Databases: B-Trees and B+ Trees used in databases and file systems for indexing.
- Search Operations: Binary Search Trees (BST) enable efficient search, insertion, and deletion operations.
Implementing a Binary Search Tree (BST) in Python
The definition of Tree
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
Init tree like this
10
/ \
5 15
/ \ / \
3 7 12 18
def insert(self, key):
if self.root is None:
self.root = TreeNode(key)
else:
self._insert(self.root, key)
def _insert(self, node, key):
if key < node.key:
if node.left is None:
node.left = TreeNode(key)
else:
self._insert(node.left, key)
else:
if node.right is None:
node.right = TreeNode(key)
else:
self._insert(node.right, key)
def in_order_traversal(self, node):
result = []
self._in_order_traversal(node, result)
return result
def _in_order_traversal(self, node, result):
if node:
self._in_order_traversal(node.left, result)
result.append(node.key)
self._in_order_traversal(node.right, result)
def pre_order_traversal(self, node):
result = []
self._pre_order_traversal(node, result)
return result
def _pre_order_traversal(self, node, result):
if node:
result.append(node.key)
self._pre_order_traversal(node.left, result)
self._pre_order_traversal(node.right, result)
def post_order_traversal(self, node):
result = []
self._post_order_traversal(node, result)
return result
def _post_order_traversal(self, node, result):
if node:
self._post_order_traversal(node.left, result)
self._post_order_traversal(node.right, result)
result.append(node.key)
def level_order_traversal(self, node):
result = []
if node is None:
return result
queue = [node]
while queue:
current = queue.pop(0)
result.append(current.key)
if current.left:
queue.append(current.left)
if current.right:
queue.append(current.right)
return result
Source Code: https://github.com/hongquan080799/data-structure-and-algorithms
Conclusion
Trees are a powerful and versatile data structure used in many real-world applications. Understanding the different types of trees and their operations is crucial for solving various algorithmic problems and designing efficient software systems. From hierarchical data representation to efficient search operations, trees provide a robust solution with their unique properties and structures.