Exploring the Graph Data Structure

Data structures are fundamental concepts in computer science that enable efficient data organization and manipulation. Today, we will delve into one of the most versatile and widely used data structures: the Graph.

What is a Graph?

A Graph is a collection of nodes, also known as vertices, and edges that connect pairs of nodes. Graphs are used to represent various real-world systems such as network, social connections, and geographical maps.

Key Characteristic of Graphs

1. Vertices (Nodes): The fundamental units or points in a graph.
2. Edges: Connections between pairs of vertices.
3. Directed Graph: Edges have no direction, they simply connect two vertices.
4. Undirected Graph: Edges have no direction, going from one vertex to another.
5. Weighted Graph: Edges have associated weights or costs.
6. Unweighted Graph: Edges do not have weights

Types of Graphs

1. Simple Graph: A graph without loops or multiple edges.
2. Multigraph: A graph that may have multiple edges between the same pair of vertices.
3. Complete graph: A graph in which every pairs of vertices is connected by a unique edge.
4. Connected graph: A graph in which there is a path between any two vertices.
5. Disconnected graph: A graph in which at least one pair of vertices is not connected by a path.
6. Cyclic Graph: A graph that contains at least one cycle.
7. Acyclic graph: A graph that does not contain any cycles.

Let’s say we build an application that allows people to be friends with one another. These friendships are mutual. If Quan is friends with Thao, and Thao is friends with Tung so Quan is friends with Tung. With normal approach we can use two-dimensional array to show that relationship

friends = [
    ["Quan", ["Thao"]],
    ["Thao", "Tung"],
    ["Hieu", "Tai"],
    ["Hieu", "Viet"],
    ["Minh", "Suong"]
]

This approach is ok but there is no quick way to identify Quan is friends with Tung. In the worse case scenario we have to loop though whole array for identify the relationships then the time complexity is O(N) this is quite slow

Lucky for us, we can you graph for describe these relationships

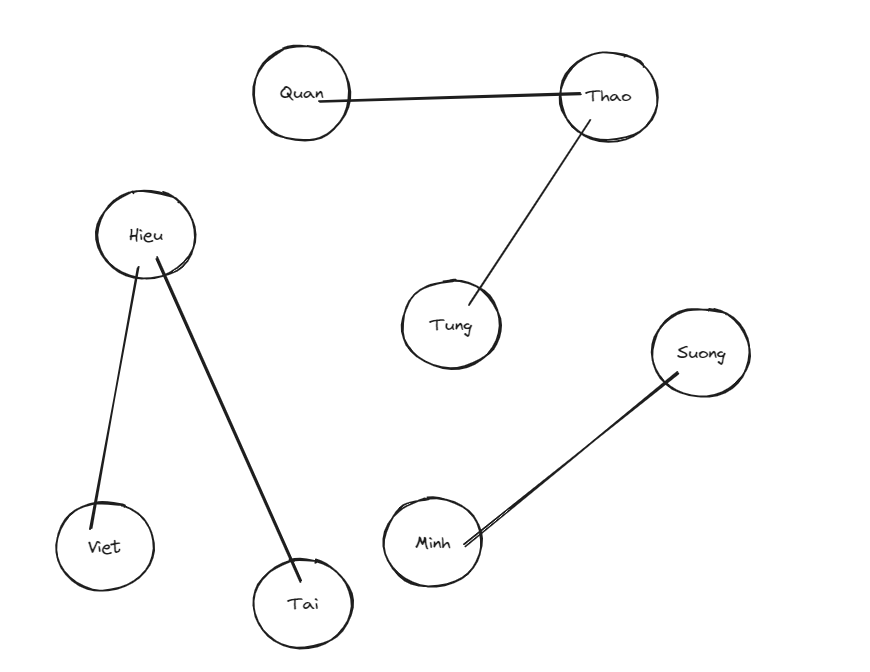
Each person is represented by a node, and each edge (line) indicates a friendship. We can quickly Quan is friends with Tung, this come with time complexity is O(1). As you noticed this look similar to Tree, actually Trees is type of graph and the differences is all trees are graph but not all graphs are trees.

Graph Representations

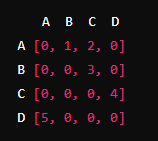
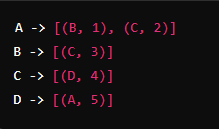
Vertices: A, B, C, D
Edges:
- A -> B (weight 1)
- A -> C (weight 2)
- B -> C (weight 3)
- C -> D (weight 4)
- D -> A (weight 5)

1. Adjacency Matrix: A 2D array where each cell represents the presence of an edge vertices
2. Adjacency List: An array or list where each element represents a vertex and contains a list of its adjacency vertices.
3. Edge List: A list of all edges, where each edge is represented by a pair of vertices.

Graph Traversal

Graph traversal refers to the process of visiting each vertex in a graph systematically. Traversal is essential for various applications such as searching, path finding, and analyzing the structure of a graph. The two most common graph traversal algorithms are DFS and BFS.

Depth-First Search (DFS)

Depth-First Search (DFS) explores as far down a branch as possible before backtracking. it uses a stack data structure, either explicitly or implicitly through recursion.

Algorithms steps”

1. Start at a given vertex (source).
2. Visit the starting vertex and mark it as visited.
3. For each adjacent vertex of the current vertex:
   • If it has not been visited, recursively apply DFS on it.
4. Backtrack to the previous vertex when no more unvisited adjacent vertices are found.

Breadth-First Search (BFS)

1. Start at a given vertex (source).
2. Visit the starting vertex and mark it as visited.
3. Add the starting vertex to a queue.
4. While the queue is not empty:
   • Remove the front vertex from the queue.
   • For each adjacent vertex of the removed vertex:
     • If it has not been visited, mark it as visited and add it to the queue.

Implementing a Graph in Python

Definition of Graph

class Graph:
    def __init__(self):
        self.adjacency_matrix = []
        self.adjacency_list = {}
        self.edge_list = []

Graph traversal

def bfs(self, start_vertex):
        visited = set()
        queue = [start_vertex]
        order = []

        while queue:
            current_vertex = queue.pop(0)
            if current_vertex not in visited:
                visited.add(current_vertex)
                order.append(current_vertex)
                queue.extend([neighbor[0] for neighbor in self.adjacency_list[current_vertex] if neighbor[0] not in visited])
        return order

    def dfs(self, start_vertex):
        visited = set()
        stack = [start_vertex]
        order = []

        while stack:
            current_vertex = stack.pop()
            if current_vertex not in visited:
                visited.add(current_vertex)
                order.append(current_vertex)
                stack.extend([neighbor[0] for neighbor in self.adjacency_list[current_vertex] if neighbor[0] not in visited])
        return order

Source Code : https://github.com/hongquan080799/data-structure-and-algorithms

Conclusion

Graphs are a powerful and versatile data structure used in numerous real-world applications. Understanding the different types of graphs, their representations, and traversal algorithms is crucial for solving various algorithmic problems and designing efficient software systems. From social networks to geographical maps, graphs provide a robust solution for modeling complex relationships and dependencies.